The Artificial Intelligence Clinician learns optimal treatment strategies for sepsis in intensive care, Nature Medicine (2018) [Paper]

Summary

• Desicion-marking for the administration of intravenous fluids and vasopressors for sepsis in ICU
• AI policy, Learned clinician policy, Zero drug policy (fixed action), Random policy
• The value of the AI Clinician’s selected treatment is on average reliably higher than human clinicians. - In the external set, mortality was lowest in patients for whom clinicians’ actual doses matched the AI decisions

Introduction

Developed the AI Clinician, a computational model using reinforcement learning, which is able to dynamically suggest optimal treatments for adult patients with sepsis in the intensive care unit (ICU). (the administration of intravenous fluids and vasopressors)
MIMIC III - development dataset, eICU - testing dataset
n = 13,666 patients in the MIMIC-III development dataset, n = 3,417 in the MIMIC-III test set and n = 79,073 in the eRI set.
Extracted 48 variables, 4-h time steps

Terminology

• AI policy: by solving MDP using policy iteration for targeting 90-d survival
• Clinicians’ policy: behavior policy generated by true trajactories

Method

Building the computational model
MDP

• S, a finite set of states (in our model, the health states of patients).
• A, the finite set of actions available from state s (in our model, the dose prescribed of intravenous fluids and vasopressors converted into discrete 25 decisions).
• T(s′ ,s,a), the transition matrix, containing the probability that action a in state s at time t will lead to state s′ at time t + 1, which describes the dynamics of the system.
• R(s′), the immediate reward received for transitioning to state s′. Transitions to desirable states yield a positive reward, and reaching undesirable states generates a penalty.
• γ, the discount factor, which allows modelling of the fact that a future reward is worth less than an immediate reward.

A sample of 80% of the MIMIC-III cohort was used for model training, and the remaining 20% was used for model validation.
Built 500 different models using 500 different clustering solutions of the training data, and the selected final model maximized the 95% confidence lower bound of the AI policy.
The state space was constructed by k-means++ clustering of the patients’ data, resulting in 750 discrete mutually exclusive patient states.
Used Bayesian and Akaike information criteria to determine the optimal number of clusters.
Two absorbing states were added to the state space, corresponding to death and discharge of the patient.
log-normal distributed variables were log-transformed before standardization, and binary data was centered on zero. The normality of each variable was tested with visual methods: quantile-quantile plots and frequency histograms.

Used either hospital mortality or 90-d mortality as the sole defining factor for the system-defined penalty and reward. When a patient survived, a positive reward was released at the end of each patient’ trajectory (a ‘reward’ of +100); a negative reward (a ‘penalty’ of –100) was issued if the patient died.

Estimated the transition matrix T(s′,s,a) by counting how many times each transition was observed in the MIMIC-III training dataset and converting the transition counts to a stochastic matrix.

Chose a γ value of 0.99.

Evaluation of clinicians’ actions (policy)
Performed an evaluation of the actual actions (the policy) of clinicians using temporal difference learning (TD-learning) of the Q function by observing all the prescriptions of intravenous fluids and vasopressors in existing records (offline sampling) and computing the average value of each treatment option at the state level.
$Q^\pi(s,a) \leftarrow Q^\pi(s,a)+\alpha(r+\gamma Q^\pi(s’,a’)-Q^\pi(s,a))$
Stopped the evaluation after processing 500,000 patient trajectories with resampling.

Estimation of the AI policy
In-place policy iteration
Policy iteration started with a random policy that was iteratively evaluated and then improved until converging to an optimal solution. After convergence, the AI policy $\pi^*$ corresponded to the actions with the highest state-action value in each state.

Model evaluation
The objective is to evaluate the value of a newly learnt AI policy using trajectories of patients generated by another policy (the clinicians’). This is termed off-policy evaluation (OPE).

Implemented a type of HCOPE method, WIS, and used bootstrapping to estimate the true distribution of the policy value in the test sets.
WIS may be a biased although consistent policy estimator, so the bootstrap confidence interval may also be biased, even though the literature suggests that consistency is a more desirable property than unbiasedness.
It is accepted that bootstrapping produces accurate confidence intervals with less data than exact HCOPE methods and is safe enough in high-risk applications.

$\pi_0$ as the behavior policy (the clinicians’) from which actual patient data was generated
$\pi_1$ as the evaluation or AI policy

Softened $\pi_1$, so it now recommends taking the suggested action 99% of the time and any of the other actions a total of 1% of the time. This allows assessment of the entirety of the patient trajectories.
The goal was to estimate the value of $\pi_1$ from data trajectories. \

Built 500 different models from various selections of a random 80% of the MIMIC-III data and evaluated the AI policies with WIS on the remaining 20% of the data.
Estimated the value of a random policy and a zero-drug policy for comparison (Fig. 2b).
The selected final model maximizes the 95% confidence lower bound of the AI policy among the 500 candidate models.

Results

Evolution of the 95% lower bound (LB) of the best AI policy and of the 95% upper bound (UB) of highest-valued clinician policy during the building of 500 models. After only a few models, a higher value for the AI policy than the clinician treatment, within the accepted risk, is guaranteed.

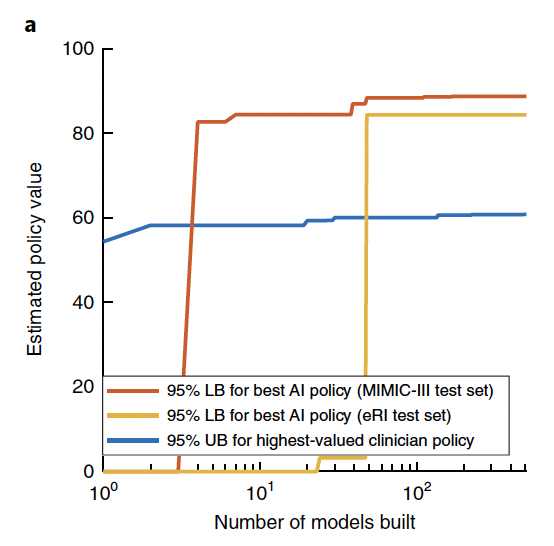
* Estimated policy value = WIS for all trajectories

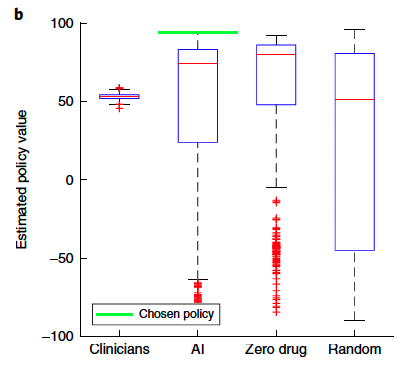
Distribution of the estimated value of the clinicians’ actual treatments, the AI policy, a random policy and a zero-drug policy across the 500 models in the MIMIC-III test set (n = 500 models in each boxplot). The chosen AI policy maximizes the 95% confidence lower bound. On each boxplot, the central line indicates the median, and the bottom and top edges of the box indicate the 25th and 75th percentiles, respectively.

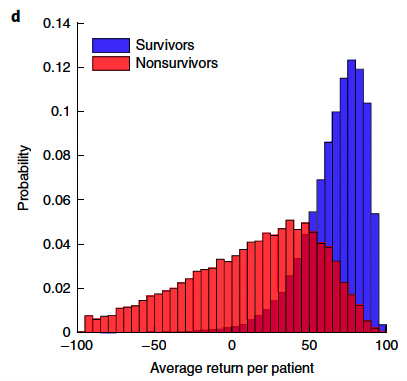
The relationship between the return of the clinicians’ policy and patients’ 90-day mortality in the MIMIC-III training set (n = 13,666 patients). Return of actions were sorted into 100 bins, and the mean observed mortality (blue line for raw, red line for smoothed) was computed in each of these bins. The shaded blue area represents the s.e.m. \

Average return in survivors (n = 11,031) and nonsurvivors (n = 2,635) in the MIMIC-III training set. c and d were generated by bootstrapping in the training data with 2,000 resamplings.

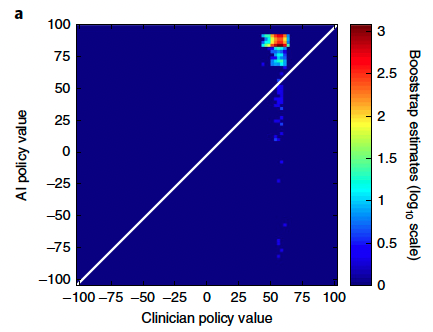
Distribution of the estimated value of the clinician and AI policies in the selected model, built by bootstrapping with 2,000 resamplings in the eRI dataset.

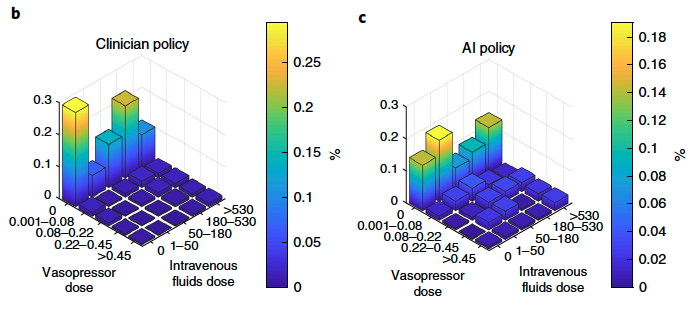
Visualization of the clinician and AI policies. All actions were aggregated over all time steps for the five dose bins of both medications. On average, patients were administered more intravenous fluid (b) and less vasopressor (c) medications than recommended by the AI policy.

The dose excess, referring to the difference between the given and suggested dose averaged over all time points per patient, for intravenous fluids (left) and vasopressor (right). The figure was generated by bootstrapping with 2,000 resamplings. The shaded area represents the s.e.m. In both plots, the smallest dose difference was associated with the best survival rates (vertical dotted line). The further away the dose received was from the suggested dose, the worse the outcome.

Question

• how to draw mortality-reward curve ?