A Gentle Introduction to Graph Neural Networks, Distill (2021) [Paper]

Only cover what’s interesting or new in my view.

Message passing examples

• by only nodes
  
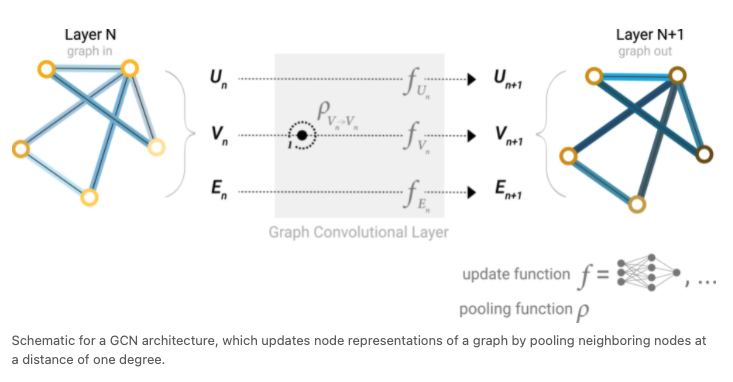
• by nodes and edges
  
  
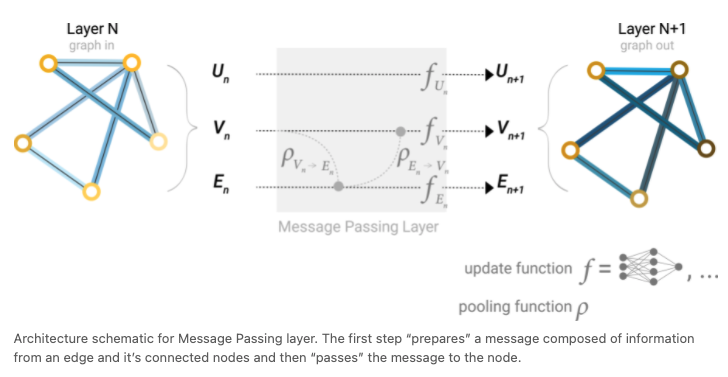
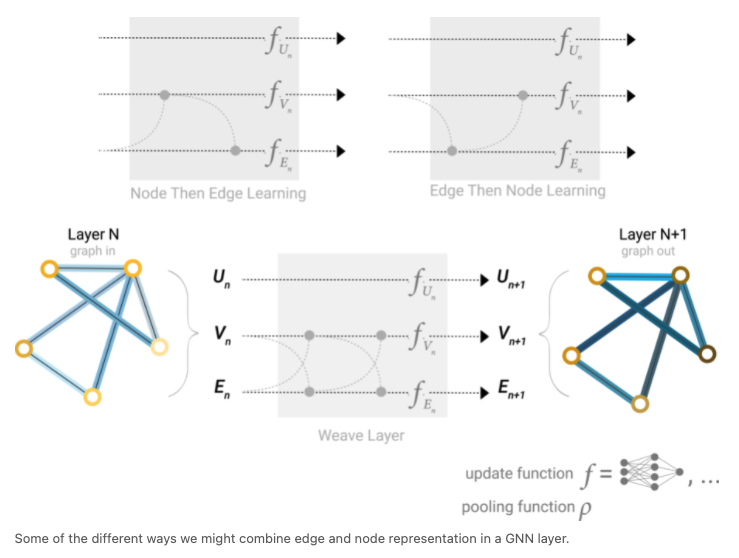
• by nodes, edges, and global representation
  
  

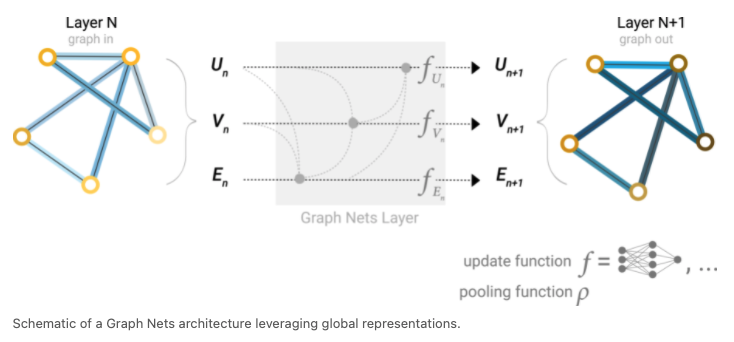
Real world practice

• Dataset: The Leffingwell Odor dataset, which is composed of molecules with associated odor percepts.
• Task: Predicts if a molecular graph smells “pungent” or not.
• node types: Carbon, Nitrogen, Oxygen, Fluorine
• edge types: Single, Double, Triple, Aromatic
• Results
  
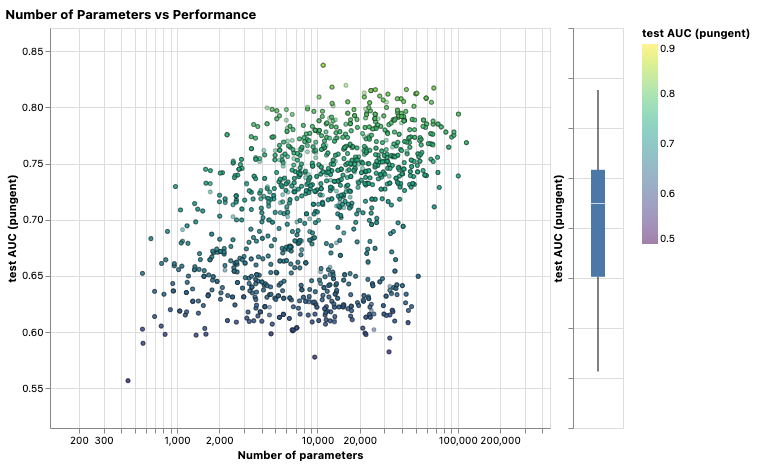
  A higher number of parameters does correlate with higher performance.
  
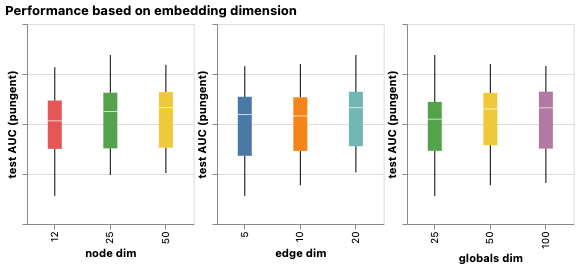
  Models with higher dimensionality tend to have better mean and lower bound performance but the same trend is not found for the maximum.
  
  The mean performance tends to increase with the number of layers, the best performing models do not have three or four layers, but two.
  
  GNN with a higher number of layers will broadcast information at a higher distance and can risk having their node representations ‘diluted’ from many successive iterations.
  
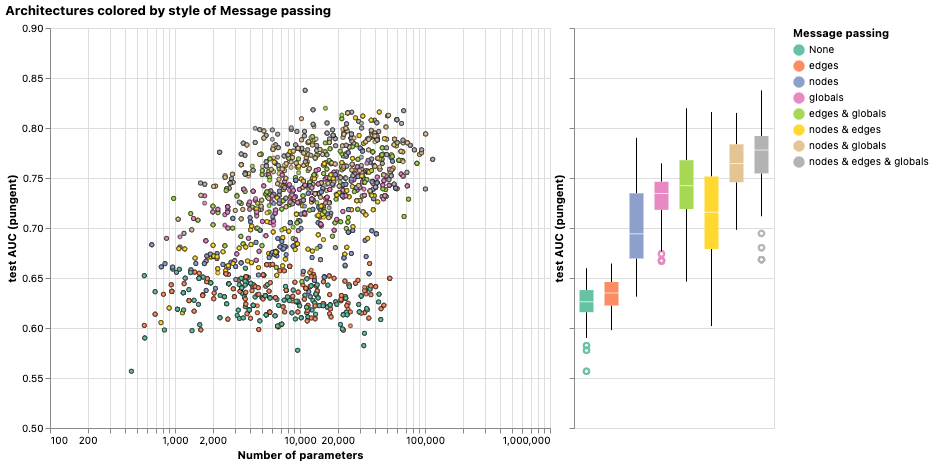
  The task is centered on global representations, so explicitly learning this attribute also tends to improve performance. The more graph attributes are communicating the more we tend to have better models

Into the Weeds

Hypernode, We can consider nested graphs, where for example a node represents a graph, also called a hypernode graph. Nested graphs are useful for representing hierarchical information. For example, we can consider a network of molecules, where a node represents a molecule and an edge is shared between two molecules if we have a way (reaction) of transforming one to the other. In this case, we can learn on a nested graph by having a GNN that learns representations at the molecule level and another at the reaction network level, and alternate between them during training.

Subgraph for Batching in GNNs, The main idea for batching with graphs is to create subgraphs that preserve essential properties of the larger graph. This graph sampling operation is highly dependent on context and involves sub-selecting nodes and edges from a graph. How to sample a graph is an open research question.

Inductive biases, we are identifying symmetries or regularities in the data and adding modelling components that take advantage of these properties. For graph, a model should preserve explicit relationships between entities (adjacency matrix) and preserve graph symmetries (permutation invariance). We expect problems where the interaction between entities is important will benefit from a graph structure. Concretely, this means designing transformation on sets: the order of operation on nodes or edges should not matter and the operation should work on a variable number of inputs.

Aggregation operations, there is no operation that is uniformly the best choice. The mean operation can be useful when nodes have a highly-variable number of neighbors or you need a normalized view of the features of a local neighborhood. The max operation can be useful when you want to highlight single salient features in local neighborhoods. Sum provides a balance between these two, by providing a snapshot of the local distribution of features, but because it is not normalized, can also highlight outliers. In practice, sum is commonly used.

Edges and the Graph Dual, one thing to note is that edge predictions and node predictions, while seemingly different, often reduce to the same problem: an edge prediction task on a graph 𝐺 can be phrased as a node-level prediction on 𝐺’s dual.